0 Algebra 1 Unit 1 Interactive Notebook Pages

My Algebra 1 students just finished up their first unit on Thursday.  This year, I am attempting to model my Algebra 1 class on the Kagan Cooperative Learning Algebra 1 curriculum.  As I'm getting to know my students, I have made some adjustments.  Okay.  I've made a ton of adjustments.  My Algebra 1 students this year seem to be at a lower level than last year's students.  Let's just say it's going to be an interesting year...

I'm so excited to share with you what my students' interactive notebooks consist of thus far!  I've embedded the files for these pages at the bottom of this post.  Hope these can be of some use to you!

Algebra 1 Interactive Notebook

Unit 1 Table of Contents

3 Requirements for a Good Definition

The Kagan curriculum I am using focuses on having students develop their own definitions for the vocabulary words for each unit.  This is an entirely new approach to me.  I'm used to just giving the students the definition and having them write it down.  I'm kinda obsessed with the Frayer Model.

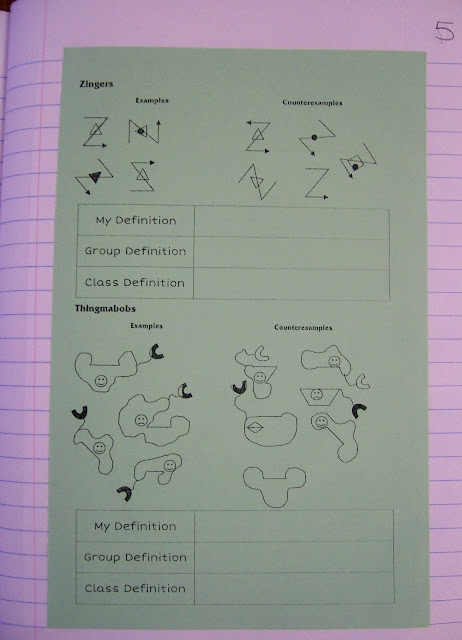
I'm enjoying the approach, however, of having students examine examples and counterexamples to determine what a word means for themselves.  Time will tell if this leads to a higher level of understanding and recall.  The first lesson of the year focused on what a good definition consists of.  Our three requirements for a good definition were: 1) states the term, 2) states the nearest classification, and 3) states those items that make it unique.

We practiced a lot with this.  I used some examples provided in the book to give my students the opportunity to practice writing a definition that had absolutely nothing to do with mathematics.  Students were given a minute or two to examine the zingers and thingmabobs.  Then, each student wrote their own definition based on the examples and counterexamples.  Next, each person in the group shared their definition with the rest of the group.  Each group discussed everybody's definition and combined the best parts of each definition into one group definition.  Finally, we discussed the group definitions as a class and wrote one class definition.  The process is very time consuming.  But, it produces AMAZING discussions.  So, I think it's worth it.

Writing Good Definitions Practice

Since I used images from this book, I cannot post these files to download.  If you are interested in these resources, you may purchase the book here.

Unit 1 Vocabulary Foldables

My students repeated this process for our 10 vocabulary words for unit 1.  They completed the "My Definition" section as homework.  And, the entire next class period was spent creating group and class definitions.  These were formatted as two book-type foldables that students glued in their interactive notebooks.  I love that these foldables capture the process that students went through to write their own definition.

The Real Number System Graphic Organizer

We summarized the real number system using the graphic organizer that I created last year.  It felt good to be able to reuse something from last year instead of creating something entirely new from scratch!

Exploring Rational and Irrational Numbers Foldable - Outside

This is a picture of a foldable that I created for my students to use as they walked through an exploration activity.  This activity did not go as planned.  I thought it would take one class period.  After one class period, we had only started to scratch the surface.  I ended up never finishing this activity with my students because I felt a need to move on.  Still, I want to share this activity with you in the hopes that someone might be inspired to take this and make it better or at least give me insight on why it didn't quite work.

This activity was created with N-RN.3 (3. Explain why the sum or product of two rational numbers is rational; that the sum of a rational number and an irrational number is irrational; and that the product of a nonzero rational number and an irrational number is irrational.) in mind.  I had some blank sticker name badges in my desk.  So, I took a Sharpie and wrote various rational and irrational numbers on each name badge.  As students came in the classroom, they got to pick a random number from the pile.  After a brief introduction to the TI-30 Scientific Calculator, students were instructed to partner up and fill out the first line of this chart.  They would fill in their number, the classification of their number (rational or irrational), their partner's number, their partner's number's classification, and the operation of addition.  Using the scientific calculator, students would add the two numbers together, record the result, and then determine whether the result was rational or irrational.  Find a new partner.  Repeat until the first five lines have been filled in.

Exploring Rational and Irrational Numbers Foldable - Inside

After completing five addition operations, we would have a class discussion.  I was hoping that students would arrive at the fact (on their own) that a rational plus a rational is always rational, an irrational plus a rational is always irrational, etc.  This went semi-well.  Some of my classes struggled with this way more than others.  None of my classes made it to division.  One class barely made it through subtraction.

Rational and Irrational Number Name Badges

What I didn't account for was the sheer amount of time that it took for my students to partner up, do the calculations, and fill out this chart.  This ended up feeling like an entire waste of a class period because it was a lot of work with very little to show for it.  I ended up doing most of the talking and discovering during our discovery period which was frustrating.

I still want to put this idea out there, though.  I think it's good to blog about the lessons that go well, the lessons that are just mediocre, and the lessons that don't go as planned.

And, yes, I'm the crazy teacher who wore a sticker around ALL DAY that read 3/8.  I put it on during first hour because I had an odd number of students.  So, I actually went through the activity with my students.  I didn't take off my sticker because I figured I would just have to make another one to wear for third hour and sixth hour.  Third hour, we had a fire drill.  Of course, I got asked by everyone I saw why I was wearing a number on my shirt.  The math teacher definitely came out in my answer as I explained that I wasn't just wearing any number, but a rational number.  Conversation ensued about what a rational number was.  Yes, I'm that teacher who takes every opportunity possible to teach my kiddos something mathematical!

Me with My Rational Number Badge

Later that morning, we had our tornado drill.  As the students huddled in the stairwell, the teachers stood in the hall.  The history teacher looked at me and said, "So, you're less than half?"  Confused, I asked her to repeat the question.  "So, you're less than half?"  Still confused, I decided that I would just agree with the history teacher and go on down the road even though I had no idea what she was talking about.  Luckily, she motioned toward my sticker, and I realized that she was referring to the fraction I was proudly wearing.  The other teachers in my building are used to my crazy methods that I use to teach math by now, so they weren't that surprised.

What did surprise me was my statistics students.  I have a class of 5 juniors who are taking statistics as their upper level math elective.  Statistics is the only class that we offer our students above Algebra 2.  These are our best and brightest math students who have chosen to take their math class at our school instead of our local Career Tech center.  Of course, they had to ask about my lovely sticker that I was wearing.  I explained why I was wearing it, and I told them about all the crazy conversations I had had that morning as a result.  What do my students decide to do?  They decide that they want to make their own stickers with numbers on them to wear around the school for the rest of the day.  There are kids who love math, and I'm so thankful that I get the chance to teach them!  (I'm thankful for my students who don't love math, too.  But, that's another post for another day!)    

Integer Operations Foldable - Outside

After using two-colored counters to derive the rules for adding, subtracting, multiplying, and dividing integers, I had my students create a four-door foldable to summarize the results of their findings.

Integer Operations Foldable - Inside

Inside, we wrote the rules for each type of problem and included several examples of each for students to refer to.

Order of Operations Graphic Organizer

 The last topic covered in Unit 1 was the order of operations.  I did not follow the approach laid out in the Kagan curriculum for this topic.  I attempted to adapt last year's interactive notebook set-up for this topic.  But, I added new activities and songs as an attempt to reach students that I felt like I had not reached during our work with integer operations.  I'm hoping that I will have time this weekend to create a post of the resources I used from other blogs to teach each major topic for this unit.  Next year, I'd love to be able to come back and find the links of all the resources I used the previous year.

Files are embedded below.  If you cannot view these files, please make sure you have Flash/Shockwave installed.  If you persist in having problems, please send me an e-mail.  I'll be happy to attach them and send them to you directly.

Unit Table of Contents


Requirements for A Good Definition


The Real Number System


Exploring Rational and Irrational Numbers



Blank 4-Door Foldable for Integer Operations Foldable


PEMDAS Graphic Organizer